Probability Concepts¶
Probability is a discipline of mathematics that studies analytical formulations of uncertainty that can be used characterize random phenomenon.
Note
PAIRED EXERCISE
Team up with the person next to you and come up with examples of two kinds of random phenomenon – one that seems like it could be predicted and one that seems like it would be difficult to predict.
Experiments¶
A sample space \(S\) is a collection, specified as a mathematical set
of all possible outcomes
that might be realized by some experiment measuring a random phenomenon.
An event \(E\) is a meaningful subset of potential outcomes of the experiment \(E \subseteq S\) that is said to have occured for a realized outcome of the experiment \(x^*\) where \(x^*\) is a member of set \(E\), i.e.,
Examples of Experiments
flip ten coins, roll two dice, draw a card from a deck
take a cookie from a cook jar, evalute an instructor, attend a meetup
measure heights, weights, volumes, temperatures, or distances
count the number of cups of coffee consumed before before 10 am
count the number of beers consumed right after this stats workshop
Examples of Outcomes
ten sequential coin flips, two die rolls, a card from a deck
a cookie, an instructor evaluation, teachers, the name of an attended meetup
a height, a weight, a volume, a temperature, or a distance
a number
hopfully not too many
Examples of Events
“Roll an even number on a 6-sided die”, “Odds”, “Spades”
“Tall people” (>2 Meters), “Frozen water (<0 C)”, “Nearby” (<1 KM)
“<2 cups of coffee before 10 am”
“NA” or “NaN”
Note
TEAM EXERCISE
Work with your neighbors to list out possible sample spaces or collection of possible outcomes for the following
Attendence at an event (class, meeting, tradeshow)
Your favorite team’s performance in the World Cup
Effects when instruments or machines are upgraded at a production facility
Set Operations¶
For events \(A\) and \(B\) defined on the sample space \(S\) of an experiment
Union: \(A \cup B = \{x: x \in A \text{ or } x\in B\}\)
is the event where either event \(A\) or event \(B\) or both occur
Intersection: \(A \cap B = \{x: x \in A \text{ and } x\in B\}\)
is the event where both the event \(A\) and the event \(B\) occur
Difference: \(A \setminus B = \{x: x \in A \text{ and } x \notin B\}\)
is the event where only the event \(A\) occurs but not the event \(B\)
Complement: \(\overline A = A^C = \{x: x\notin A\}\)
is the event that event \(A\) does not occur
The Null (Empty) Set: \(\emptyset\)
is the event that contains no outcomes, which can’t happen if the experiment is run. Sometimes intersections and differences result in empty sets.
Note
GROUP DISCUSSION
Think about safety data from field operations at a company that works with potentially dangerous machinery. Incidents may be tagged as: mechanical failure, human error, injury occured, training oversight and more.
If you want to work out the probability of certain types of events you may need to perform some set operations.
Come up with an example of where you would need:
Union
Intersection
Difference
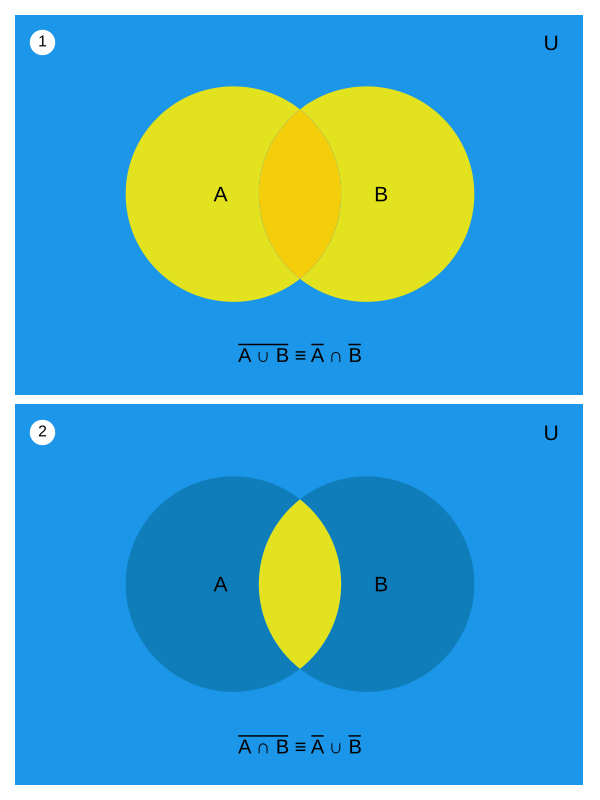
De Morgan’s Laws¶
De Morgan’s laws are tautologies that say for events \(A\) and \(B\):
1. The complement of the union of two sets is the same as the intersection of their complements:
2. The complement of the intersection of two sets is the same as the union of their complements:
where the expressions utilize the standard logic notation of \(\vee\) and \(\wedge\) for the or and and operators, respectively, and \(\neg\) for the negation operator (“not”).
The truthfulness of De Morgan’s laws can be examined using a Venn diagram:
Note
EXERCISE
Copy the following 3 lines into a python interpreter, ipython session or script
>>> a = set(["A","B","C","D"])
>>> b = set(["C","D","E","F"])
>>> sample_space = set(["A","B","C","D","E","F","G"])
and try out these set operations
>>> a.intersection(b)
set(['C', 'D'])
>>> a.difference(b)
set(['A', 'B'])
>>> a.union(b))
set(['A', 'B', 'C', 'D', 'E', 'F'])
>>> complement_a = sample_space.difference(a)
Can you demonstrate De Morgan’s laws in Python?
Random Variables¶
A random variable \(X\) is a function that maps outcomes \(s\) from its sample space \(S\) onto the real numbers \(x \in \mathbb{R}\), i.e.,
where standard notation utilizes capital letters for random variables, and lowercase letters for actualized observations (realizations) of random variables.
The realizations \(x\) of a random random variable \(X\) are dictated by the probabilities assigned to the outcomes comprising the sample space \(S\). I.e., for some event \(E \subseteq \mathbb{R}\) defined with respect to the random variable \(X\)
Random variables (Khan academy)
Putting It All Together¶
If you’re feeling ready, let’s challenge your understanding of the concepts you’ve learned thus by introducing a new concept called mutual exclusivity.
Two events \(A\) and \(B\) are said to be mutually exclusive if
Note
EXERCISE
Let \(X\) be a random variable which actualizes a cholesterol measurement and let \(x\) an actual cholesterol measurement and define the following three events
where \(A\) and \(B\) are mutually exclusive, but \(A\) and \(C\) are not.
Discuss what it means to be mutually exclusive.
What is the union of sets \(A\) and \(C\)? And how about \((A \cup B)\) = ?
If \(Pr(X=x\in A) = 0.2\) and \(Pr(X=x\in B) = 0.1\), then \(Pr(X=x \geq 250)\) = ?
How would you specify the above probability using \(A\), \(B\), \(\cup\), and \(Pr()\)?
[Extra] If \(P(X=x\in A) = .3\) and \(P(X=x\in C)=.2\), then what would you need to know to calculate \(P(X=x \leq 300)\)?
Further study¶
If you want to learn more about working with sets in Python, see:
https://www.programiz.com/python-programming/set
If you want to know more about sets and set operations in general then check out the Khan academy video series on sets, see: